# nand2tetris, Part 2.1
2022-08-25
Last week I completed nand2tetris part 1 and wrote [a blogpost about
it](nand2tetris_1.md). It was great fun; I like how I built a computer
from NAND gates. Without missing a beat I went on to work on the sequel:
nand2tetris, Part 2.
So we have a computer. Now what? Hang it on the wall for the lolz? Of
course not — let's force the emulation of silicon to think.
Again, this course expects you to finish 6 projects (actually 7 but
"module 0" is actually a replica of project 04 from part 1). As of the
time of writing, I've finished two of them. Over time I discovered that
these two projects alone are already complicated enough. If I were to wait
until I finish all six, I won't have the motivation to cover them in one
single monolithic blogpost. I find it more sensible to mark a checkpoint,
write a blogpost, then carry on doing project 09.
__SPOILER WARNING: this blogpost contains my solutions to many challenges.
If you haven't taken the course but wish to, please do it before reading
this.__
## Stack machine
Let's pull out an inventory of things we made in project 06:
- A computer built on the HACK architecture
- HACK assembly language
- An assembler from HACK assembly to machine code
What do we do now? Write Tetris in assembly? Of course not. We need
a high-level language and a compiler. However, the authors find the curve
too steep from assembly to a high-level language. Therefore, we are
introduced an abstraction: the __stack machine__, also called virtual
machine (VM). Our ultimate task in project 07 and 08 is to write a VM
translator that translates VM commands into one single assembly file,
where we emulate the stack machine on HACK hardware.
What's a stack? Sure, it's a kind of data structure, but right now we are
talking about a bunch of contiguous words in RAM and a pointer to the top.
The stack starts at RAM[256] and goes on until 2047. RAM[0], which in our
assembler is also called SP, contains the pointer to the top of our stack
(although technically, it is the address of the topmost word plus one;
more on that later). Initially, since the stack is empty, SP = 256.
Of course, our machine is much more than that, even in our first two
projects. Our focus in this blogpost is to understand how the stack
machine works, how it helps our computer be a computer, and how we
implement it using HACK assembly.
Our complete RAM is charted as follows. It'll prove useful sooner or
later.
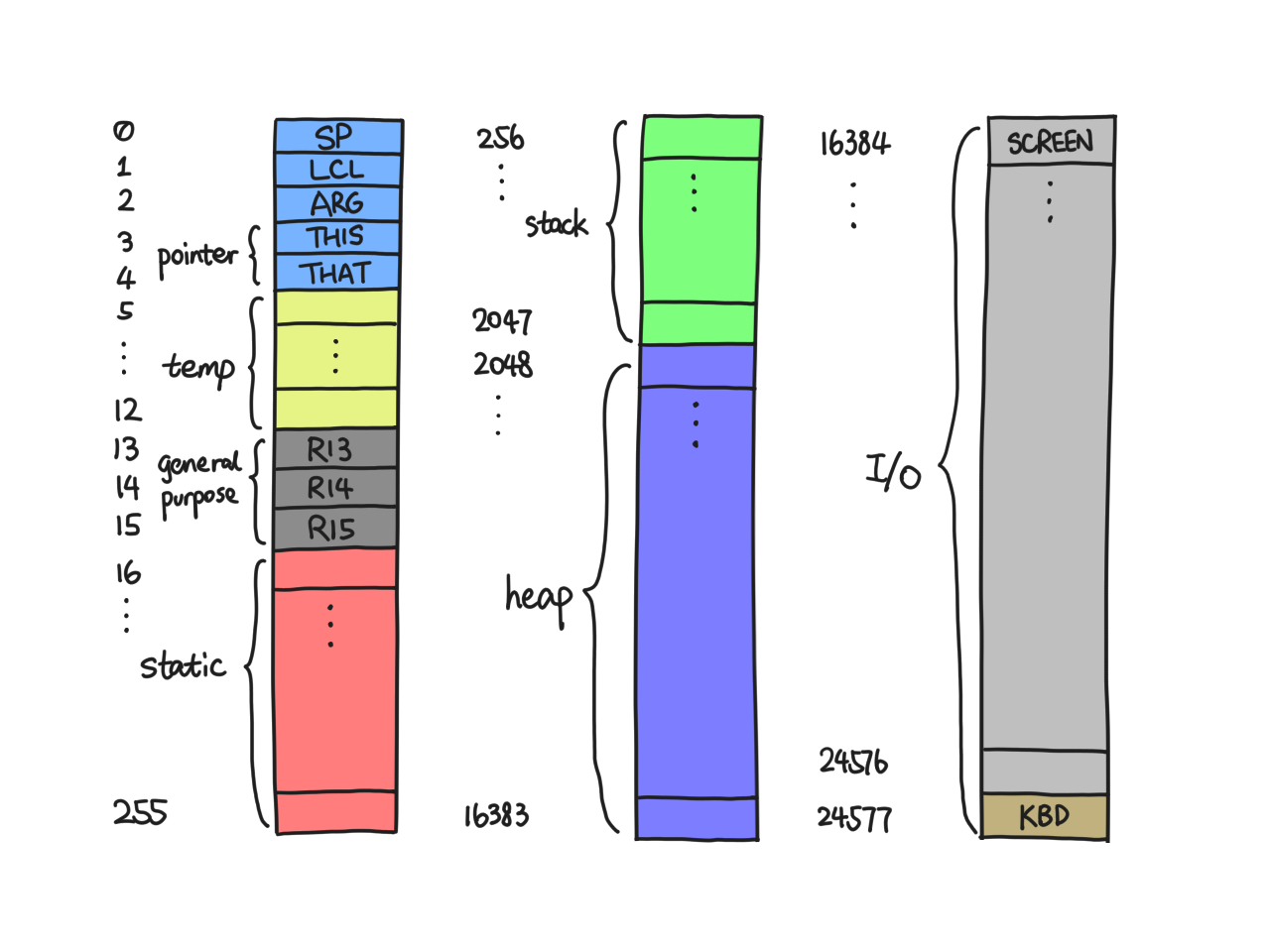
Nomenclature: Except in assembly code, the symbols SP/LCL/etc. refer to
the value stored in RAM[0]/RAM[1]/etc., and an asterisk followed by
a symbol (with or without an offset) dereferences it in C-style, e.g.
\*(LCL+1) refers to RAM[LCL+1], i.e. RAM[RAM[1] + 1].
## Memory segments
You can do many things to a stack, but the most elementary operations are
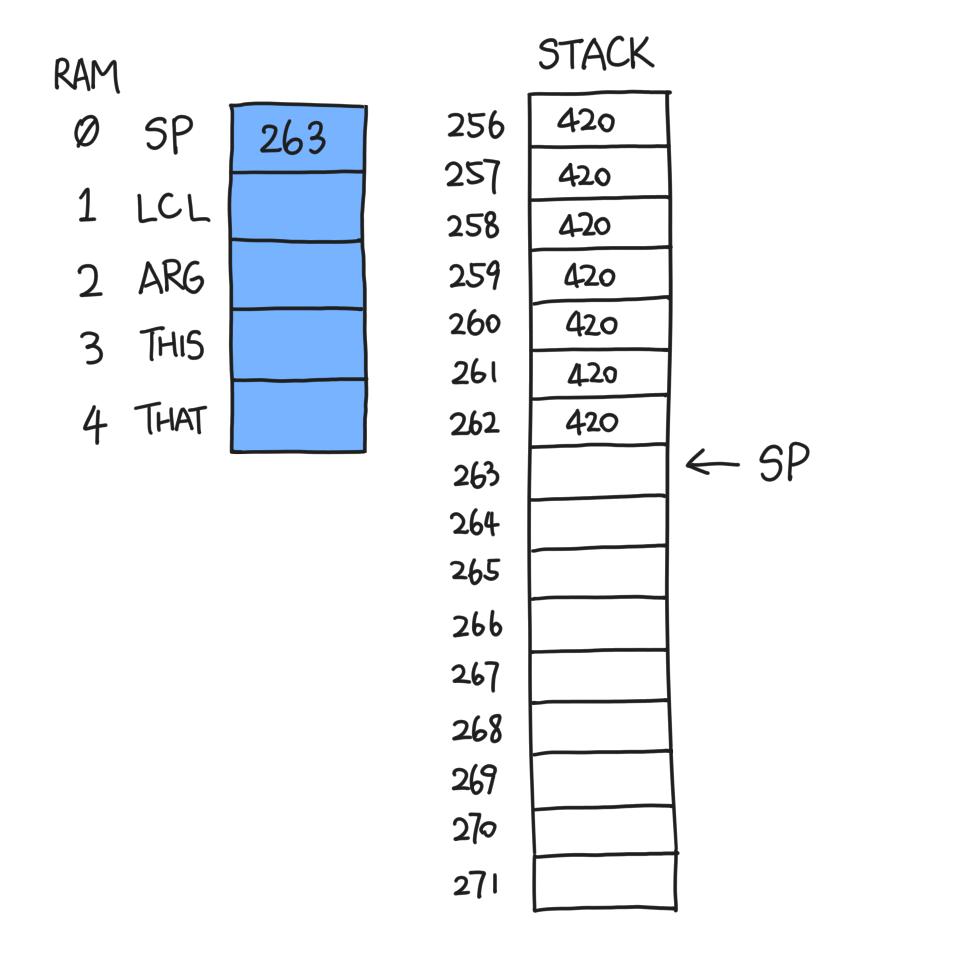
push and pop. Let's say you want to push a number, say 420, onto the
stack. All you need to do is:
- read SP
- go to RAM[SP]
- write 420
- increment SP by one
The VM command for this is `push constant 420`. You can repeat this as
many times as you please, and SP will keep updated.
What if we need to push some non-constant number, like RAM[420]? In this
case, the VM implementation imposes some restrictions. You cannot just ask
for any memory in RAM; you have to specify one of eight "memory segments".
Four of them have something to do with the four companions of SP: LCL,
ARG, THIS, and THAT. In project 06, their purposes were not clearly
stated, but they're actually pointers to useful chunks of memory at
a certain point in the program. To push them onto the stack, you follow
these pointers.
Suppose LCL (RAM[1]) is 420, and I run this VM command: `push local 3`.
The result is:
- SP is incremented by one
- \*(SP-1) is equal to RAM[420+3]
LCL is not an assemble-time constant, so the 420+3 is computed in
runtime like this:
```
@LCL
D=M // D is 420
@3
A=D+A // A is 423
D=M // now D is RAM[423]
```
The other memory segments are dead simple so I will not elaborate.
pop is the exact opposite of push and share a similar syntax. It's worth
mentioning that:
- You decrement SP _before_ copying top of stack to memory segment
- There's no need to erase what you just popped from the stack
- You can't pop to the constant segment
__Watch me struggle to implement `pop local 3`__
All I have to do is copy \*(--SP) into \*(LCL+3) in assembly. Easy, right?
Here goes:
```
// find out what's on top of stack
@SP
AM=M-1
D=M // D = RAM[SP]
// go to destination
@LCL
D=M
@3
A=D+A
M=D // RAM[LCL+3] = D
```
Do you spot the problem? When we did `D=M` the second time, we overwrote
our copy of \*SP with LCL. And that's bad, because we will need \*SP on
the last line.
The solution is a bit convoluted. You need to:
- add 3 to LCL
- decrement SP by one
- copy \*(SP) into D
- go to \*LCL
- write D into \*LCL
- subtract 3 from LCL
The main difference is that we no longer touch D as we relay the data. The
assembly is 14 instructions long, compared to 10 when we do `push local
3`, as a result of this limitation I call "not enough registers".
I would like to thank John Downey for [his
implementation](https://github.com/jtdowney/nand2tetris/blob/master/07/commands/pop_command.rb)
which I referred to when I was stuck.
OK, so we're done with pushing and popping. It doesn't sound very
exciting, does it? After all it's just copying and pasting stuff into more
stuff. Indeed, we need to discover what we can do with our stack.
## Stack arithmetics
When we program, we will need to do math at one point (gasp, who could've
thought that). Thus, we will be implementing `add`, `sub` and `neg`. These
commands do not take "parameters" like push and pop do because they always
operate on the top of stack. Suppose we have two numbers, a and b, with
b being the topmost word on our stack, i.e. \*(SP-1).
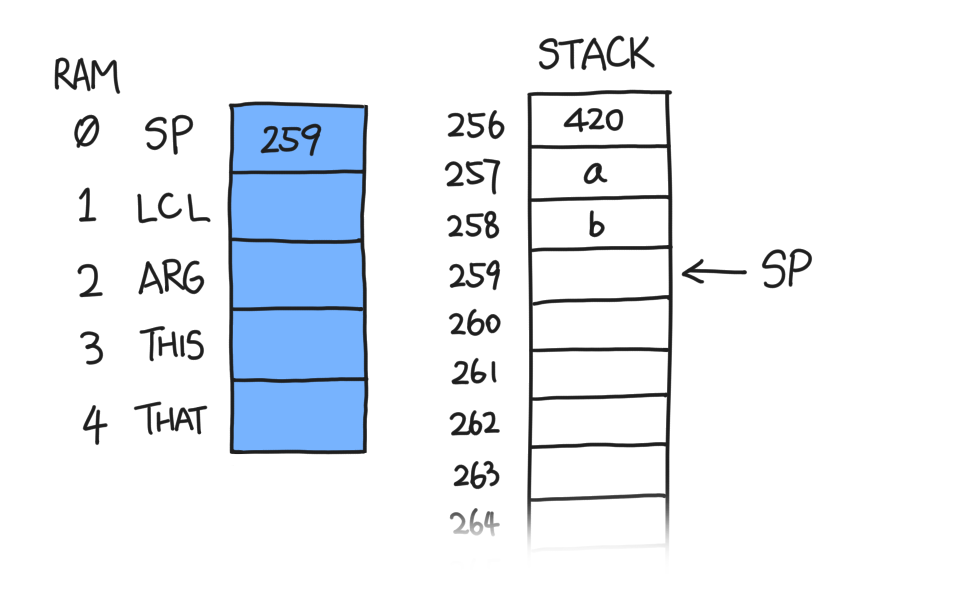
After we do `add`, the stack becomes this:
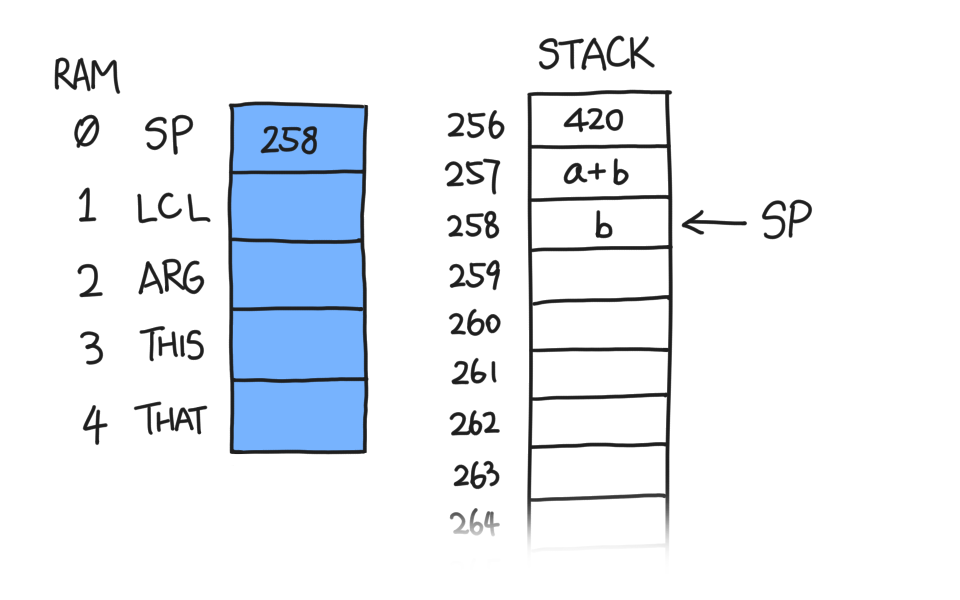
Similar to `pop`, stack arithmetic commands do not erase anything at or
after the SP marker because the stack machine only cares about what is
_in_ the stack, i.e. from 256 to SP.
Now it should be clear what `sub` does; instead of a+b, it pushes a-b.
`neg` only takes one value, so the effect is the top of stack gets
negated, i.e. b becomes -b.
## Logical commands
I classify the so-called logical commands into two categories:
- Bitwise operators: `and`, `or`, and `not`
- Comparison: `lt`, `gt`, and `eq`
### Bitwise operators
According to Shocken, logical commands return booleans. There are two
problems with this statement:
1. Booleans are indistinguishable from integers on the hardware layer;
2. _How much is a boolean?_
Without thinking I assumed false is 0 and true is 1, as in `stdbool.h`.
However, upon testing the CPU emulator told me that, in fact, true is -1,
or 65535. Not a single word was said about this specification in the
lectures. I suppose the authors had this written in their book somewhere
but forgot about it in the videos.
__In hindsight, this is obvious__
Suppose false is 0 and true is 1:
```
false = 0000 0000 0000 0000
true = 0000 0000 0000 0001
```
Now we do some logical commands:
```
false & true = 0000 0000 0000 0000 = false
false | true = 0000 0000 0000 0001 = true
```
So far so good, but problems arise as soon as we do a bitwise NOT, which
is the only native instruction related to inverting a boolean:
```
~false = 1111 1111 1111 1111 = true, probably?
~true = 1111 1111 1111 1110 = definitely not false
```
Thus we have proven that, if true is 1, a bitwise NOT does not invert it
to false. For this to happen, true has to be 16 ones, i.e. -1.
### Comparison
We proceed to implement the comparison commands: `lt`, `gt`, and `eq`.
Apparently they are extremely similar in logic:
- Pop topmost word on stack into D (SP is decremented whenever I say
"pop")
- Pop and subtract the new topmost word from D
- Compare D to zero
- Push true to stack if [condition], false otherwise
There are two things to figure out at this moment:
- What is [condition] for each of the three commands
- How do we make this "if … otherwise …" work
To be honest, I was reluctant to use branching in assembly because if so
I would have to generate a lot of labels. After quite a while messing with
the D register trying to find an "elegant" solution, I quit. Branches are
not that bad.
__Sample assembly for `lt`__
Suppose the stack is once again in this state:

```
@SP
AM=M-1 // SP--
D=M // D = b
A=A-1
D=M-D // D = a-b
M=0 // RAM[257] = false
@END_LT_0
D;JGE // if (D >= 0) goto END_LT_0
@SP
A=M-1
M=-1 // RAM[257] = true
(END_LT_0)
```
## Function commands
No language is practical without functions. Although I cannot be more
familiar with the notion of functions, the implementation remains
a mystery. The fascinating thing about functions it that it is not
a simple goto; the program has to return where it came from. In other
words, every function call involves a context switch, which will be
reversed once it returns.
Suppose we are in function f(x), and we're calling g(y). We are going to
have two states: one used by f just before g is called, and one used by g.
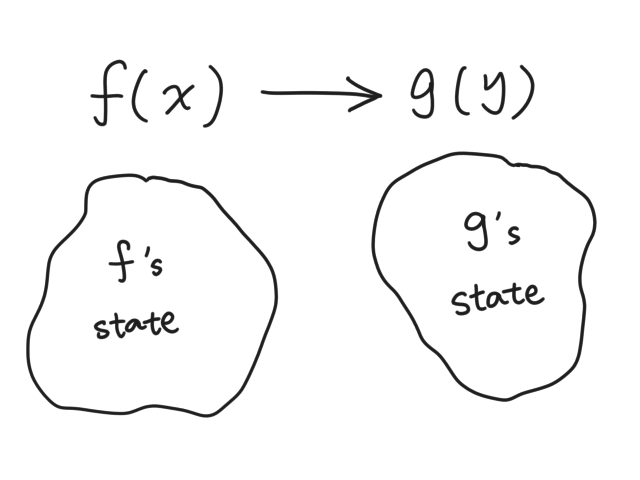
What's in a function's state? As it turns out, it's four pointers and one stack:
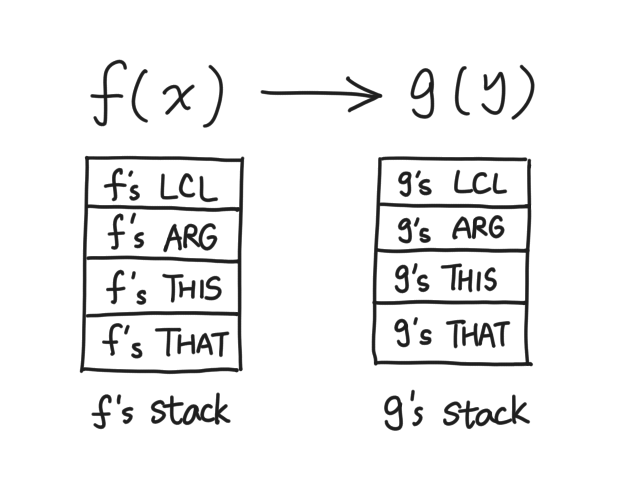
The neat thing about our VM is that, there's only one global stack, and
the stack of each function just starts somewhere in the middle, instead of
256.
Suppose I, function f, am about to call function g at a point in time when
SP=301. I must first push the arguments it needs, let's say 60 and 9:
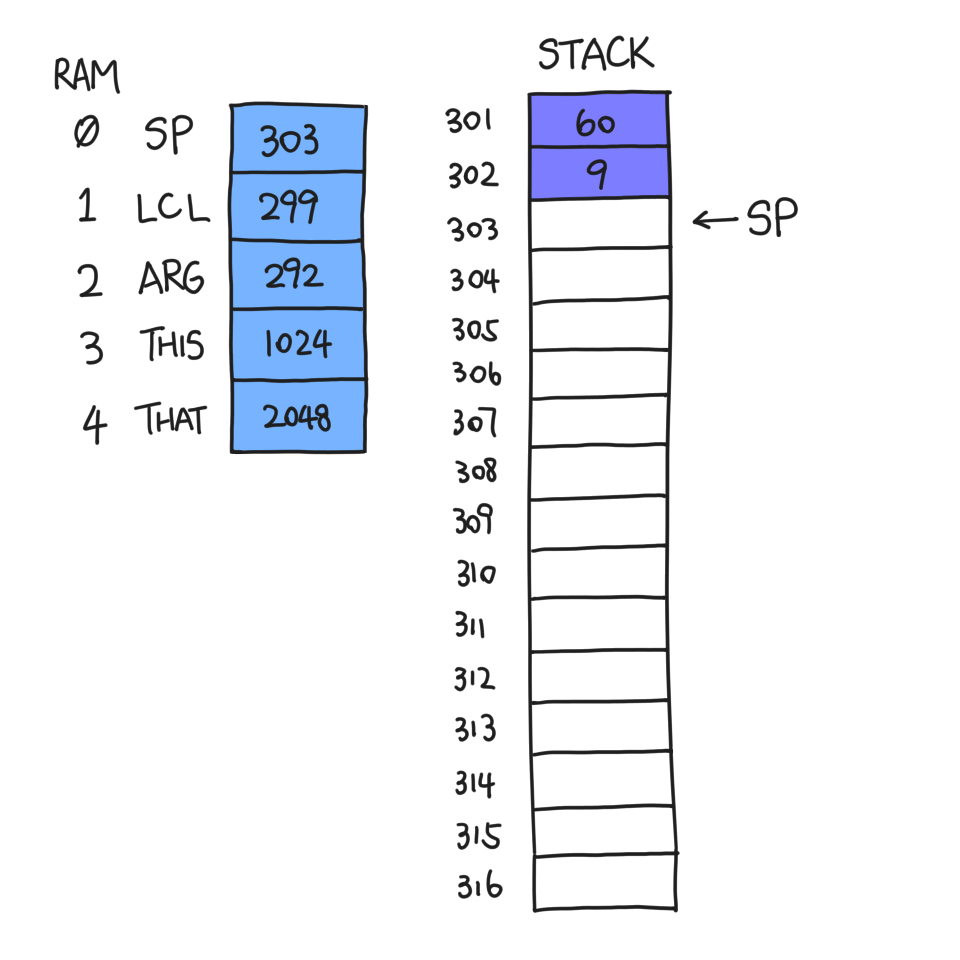
Now, I execute `call g 2`, where the 2 is the number of arguments that
g takes. But before I do anything risky, I need to back up my state. One
of them is the "return address", which is the address of the instruction
I would be executing next if I didn't call g.
__Wait, you're telling me we're predicting the future?__
It sounds like wizardry but it's not. This is done with the assembler's
symbol substitution: I insert a label (for example, `(Main$ret.0)`) just
before the first instruction of the next VM command. This is where I'll
end up if `call g 2` wasn't there. Knowing the assembler will take care of
this, I just write:
```
@Main$ret.0
D=A
@SP
A=M
M=D // *SP is the return address
@SP
M=M+1 // SP++
// more code
@Main.g
0;JMP
(Main$ret.0)
// assembly translated from next VM command
```
If `0;JMP` is instruction 419, then the return address pushed is 420.
Then we just push LCL, ARG, THIS and THAT:
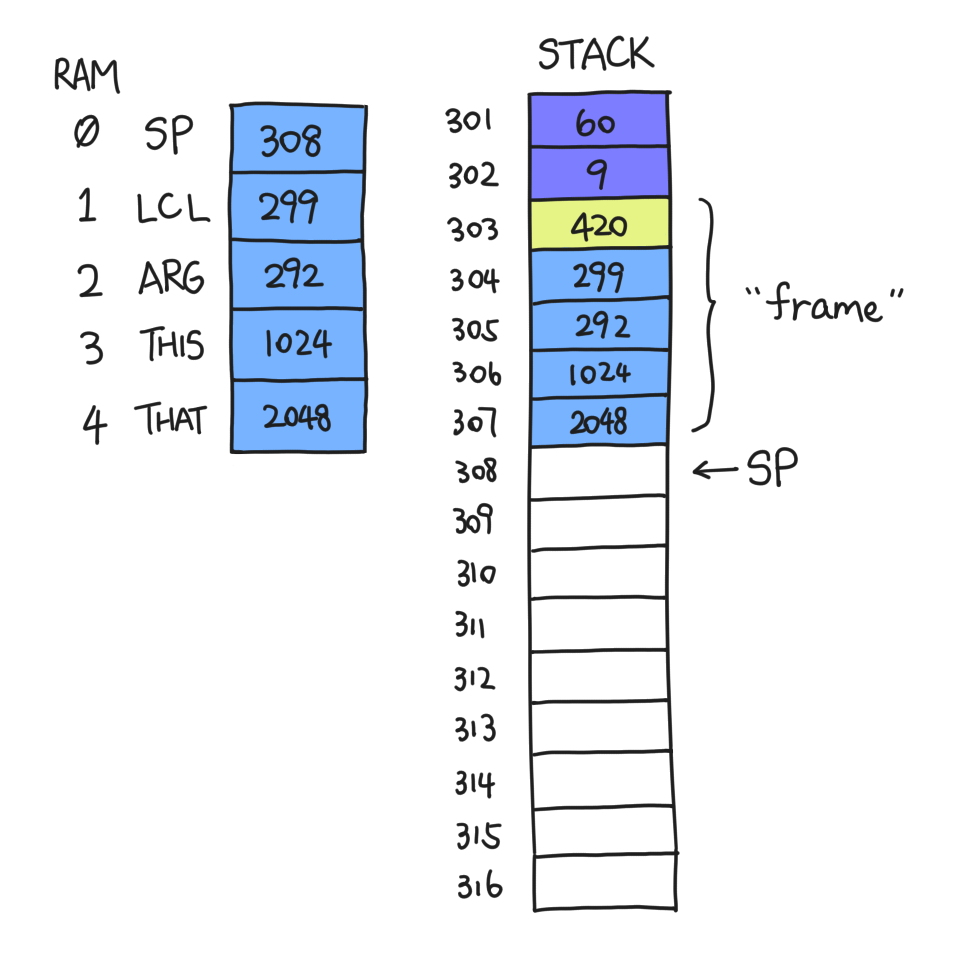
The section of memory from 303 to 307 (inclusive) is called the "frame" of
f, because it contains all the information needed by f to recover its
state.
Now that the clones of LCL et al. are safely contained within the frame,
we can commit all sorts of atrocities to them. ARG will become the address
of the first argument pushed onto f's stack, namely 301; LCL will become
the first address after the frame ends. We will not be touching THIS and
THAT just yet.
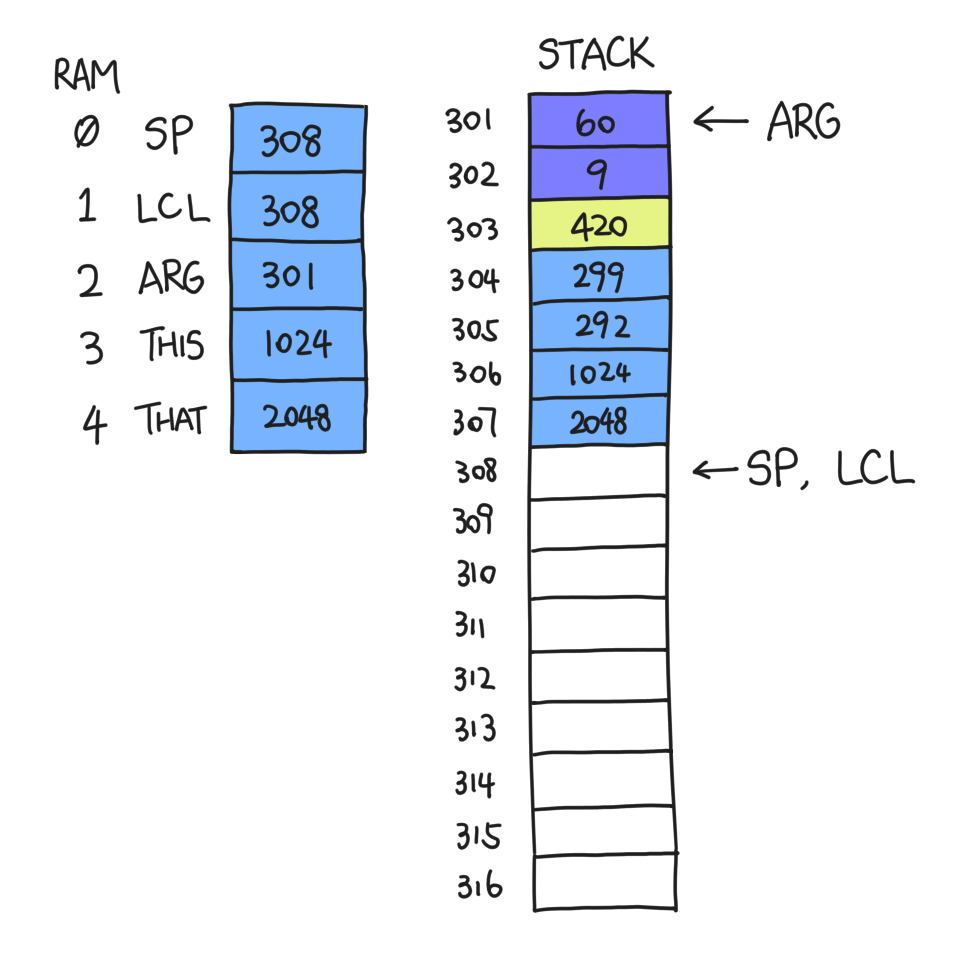
At this point f is ready to jump to g. Suppose function g begins with this
VM command: `function g 3`. The 3 here is not the number of arguments.
Instead, it's the number of local variables it needs. Therefore, this VM
command pushes this number of zeroes onto the stack:
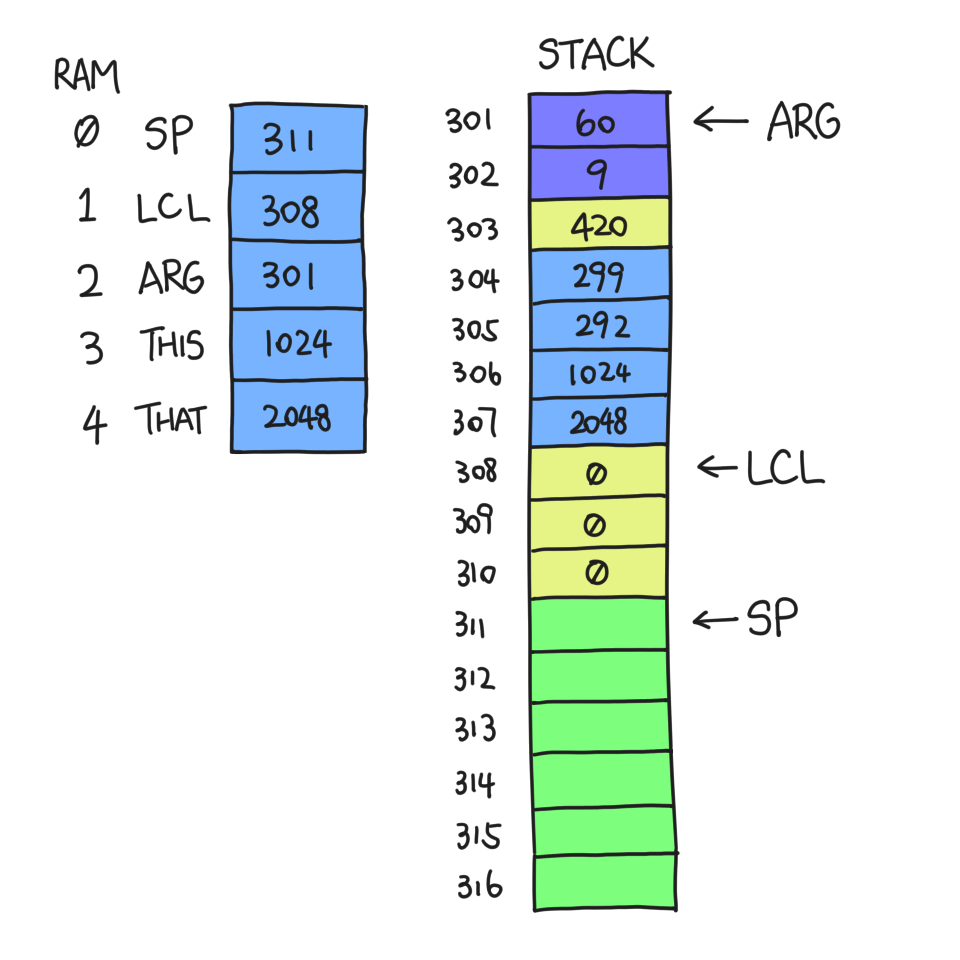
From now on, RAM[311-2047] is the stack that g has access to. It can also
access `argument 0-1` and `local 0-2`.
A dozen commands later, g decides to return. First it copies its topmost
word on stack — the return value — to somewhere convenient for f to use.
Then it exits and hands the control back to f. But in fact, g has no idea
it came from f; it only knows where to find and recover the pre-saved
context.
Suppose g pushed a few things and touched some local variables, and
decides to return.

The return value is 3519, and we know that before g was called SP was 301
— always equal to our current ARG. So we copy \*(SP-1) to \*ARG.
When the number of arguments is zero, \*ARG happens to be where we store
the return address, namely 420. We could overwrite it and lose context!
That's why we need to back up the return address somewhere safe and
recover from there; I selected R13 in my implementation and I've had no
problems yet.
After this is done, everything after LCL is useless. So we move SP to LCL:
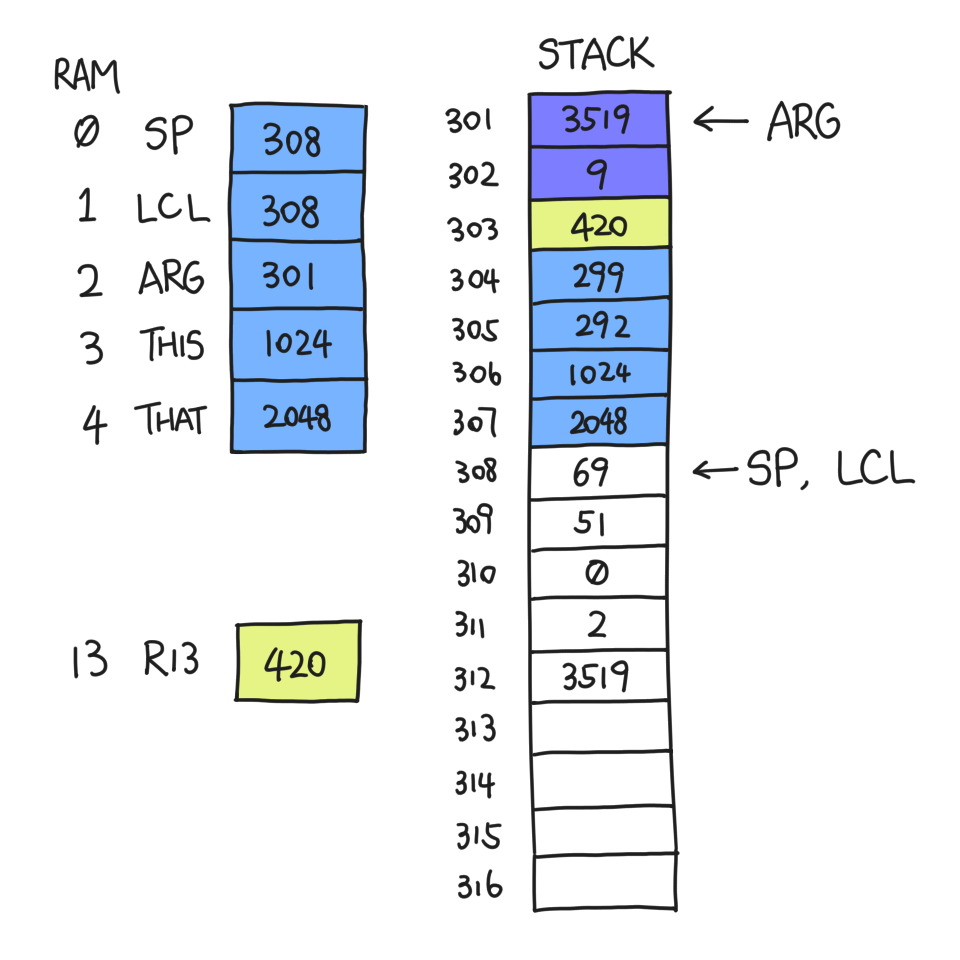
Then, we restore LCL et al. by popping them one by one, and move SP right
after the return value.

Finally, we jump to the address indicated by R13, which is 420. And thus,
this grand waltz of function call and return is complete.
## Writing the VM translator
As a person with limited wits and patience, I decided to write the VM
translator in Python 3.10 to leverage the power of pattern matching, aka
`match case`, as defined in [PEP 636](https://peps.python.org/pep-0636/).
This means I can match VM commands like
```
match cmd.split():
case []:
continue
case [("push" | "pop") as action, segment, index]:
# handle memory command
case [("add" | "sub" | "neg" | "and" | "or" | "not") as command]:
# handle arithmetic / logical command
# more cases here
case _:
# invalid command, raise error
```
This level of syntactic elegance is, in my opinion, unmatched among all
languages (pun intended). One other characteristic of the VM translator is
that it's context-free. In contrast, the assembler I wrote in project 06
needs to read the entire file to decide whether a given symbol is
a reference to a label or a variable. However it does depend on _some_
global state, for example to generate unique labels for each `lt` command.
Over the course of implementation, I realized that the hardest part is
that you are programming in two languages at once. You are using one
language to generate another. Of course, assembly is way harder (I forgot
`A=M` _multiple times_, and instead of debugging for hours in the CPU
emulator you should probably recheck if your assembly matches your
pseudocode in terms of pointer dereferencing). But the caveats in Python
showed up in unexpected places. For example, my optimized implementation
of `function ` consists of three parts: snippet A, snippet
B repeated (varc - 1) times, and snippet C. As you can imagine, things
took a dramatic turn as varc approaches zero. It turns out Python does not
raise an exception when I do `snippet_b * (-1)`; it silently returns an
empty string, which means at least one variable is initialized no matter
what. The bug is fixed, but I learned one more reason why Python is weird.
### Code statistics
- 408 lines of code
- About half of it is multiline strings of assembly
## Is the stack machine any good?
The stack machine, or any kind of virtual machine used by industrial
languages, is an intermediate step from high-level source code to machine
code. Not every languages needs it, though; C is a counterexample. Virtual
machines offer you one more level of abstraction, at the cost of
efficiency and size.
__One example how VM increases executable size__
Let's say we need to do:
```
push constant 1337
pop local 69
```
Our VM translator would output these lines:
```
// push constant 1337
@x
D=A
@SP
A=M
M=D
@SP
M=M+1
// pop local 69
@69
D=A
@LCL
M=M+D
@SP
AM=M-1
D=M
@LCL
A=M
M=D
@69
D=A
@LCL
M=M-D
```
This is 21 instructions, but in reality, some instructions are totally
unnecessary. Like when we incremented, then decremented SP. If we treated
the two commands as one atomic operation and rewrite the assembly from
scratch:
```
@69
D=A
@LCL
M=M+D
@1337
D=M
@LCL
A=M
M=D
@69
D=A
@LCL
M=M-D
```
Down to 13 instructions now.
The merit of a half-human, half-machine abstraction is increased control
and security. Suppose a function declares itself as `function f 4`, but
asks us to `pop local 9`. The VM translator could, in theory, refuse to
assemble the code, which could be malicious (if it even runs, that is).
But my VM translator does not, because I want to keep my VM translator as
simple as possible. Furthermore, the VM acts as a better troubleshooting
tool than assembly for your compiler.
## Conclusion
In project 07 and 08 of nand2tetris part 2, we built a VM translator that
translates an imaginary architecture to a concrete one. This added layer
of abstraction bridges the gap between high-level source code and machine
language. In this course, we discussed the benefits and costs in the
Perspectives unit; however, specifics are out of scope.
Philosophically, the lesson I learned is that in modern computer
engineering, universality often beats efficiency. The stack machine is
clever in that it is a complete abstraction of assembly. In other words,
everything you expect a computer to do, if you don't care about speed, can
be done on a stack machine, without the need to write a line of assembly.
Incidentally, this also describes high-level languages. Efficiency is
lost, yes, but there exist two justifications:
1. Most applications are not efficiency-critical, and if yours is
extremely so, you probably shouldn't be using a VM;
2. If you _really_ need efficiency on VM, you can revise your translator
to generate more efficient assembly.
I would like to say the following about this course:
- Shocken spoke in _every_ single lecture. Impressive.
- I'm not sure if I'm the only one, but I find the video lectures a lot
more repetitive than those in part 1.
- At least one technical specification (booleans) was not communicated
well.
- The project is arguably more challenging (intellectually, not
syntactically) than writing the assembler.
That's all for project 07 and 08; see you in Part 2.2!